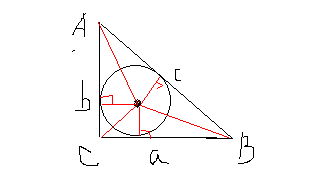
三角形内切圆半径公式是什么?
三角形内切圆半径公式:r=2S/(a+b+c)。
推导:设内切圆半径为r,圆心O,连接OA、OB、OC,得到三个三角形OAB、OBC、OAC。
那么,这三个三角形的边AB、BC、AC上的高均为内切圆半径r。
所以:S=S△ABC=S△OAB+S。
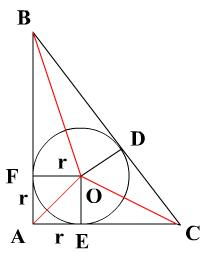
三角形内切圆的半径是怎么求的呢?
一般三角形内切圆半径为:r=2S/(a+b+c),S是三角形的面积公式 在三角形中,三个角的角平分线的交点是内切圆的圆心,圆心到三角形各个边的垂线段相等。
内切圆的半径为r=2S÷C,当中S表示三角形的面积,C表示三角。
三角形内切圆半径公式
内切圆半径公式为r=(a+b-c)/2(a,b为直角边,c为斜边)一般三角形:内切圆半径为r=2S/(a+b+c),S是三角形的面积公式。
公式推导首先画一个三角形以及三角形的内接圆,分别连接圆心和三角形三个顶点(这时可见三。