圆周角定理

圆周角定理的定理证明

　　圆周角定理：一条弧所对圆周角等于它所对圆心角的一半 证明：已知在⊙O中，∠BOC与圆周角∠BAC同对弧BC，求证：∠BOC=2∠BAC.证明：情况1：如图1，当圆心O在∠BAC的一边上时，即A、O、B在同一直线上时：∵OA、OC。

圆周角定理及其推论

　　18圆周角定理指的是一条弧所对圆周角等于它所对圆心角的一半。
　　这一定理叫做圆周角定理。
　　定理推论指的是在同圆或等圆中，同弧或等弧所对的圆周角相等，相等的圆周角所对的弧也相等。
　　定理内容:圆周角的度数等于它所对弧上。

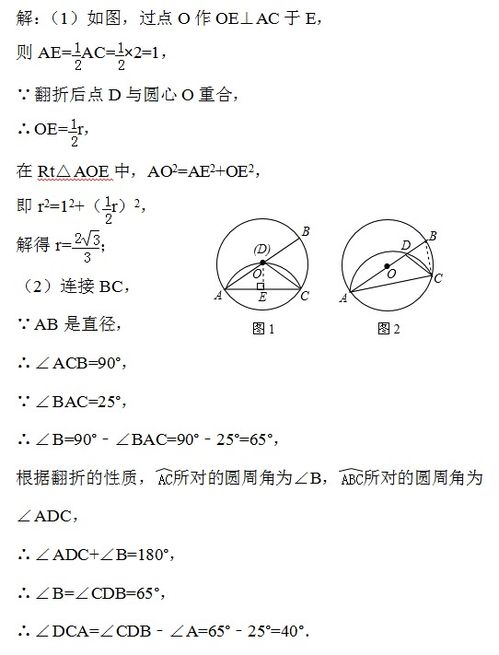
圆周角定理是什么

　　圆周角定理指的是一条弧所对圆周角等于它所对圆心角的一半。
　　这一定理叫做圆周角定理。
　　该定理反映的是圆周角与圆心角的关系。
　　1.一条弧所对的圆周角等于它所对的圆心角的一半；圆周角图 2.圆周角的度数等于它所对的弧度。

什么是 圆周角定理 ?

　　圆周角定理，就是等弧所对的圆周角是它所对的圆心角度数（或这条弧的度数）的一半

圆周角公式

　　圆周角公式：A=vf*kl。
　　圆周角定理指的是一条弧所对圆周角等于它所对圆心角的一半。
　　这一定理叫做圆周角定理。
　　该定理反映的是圆周角与圆心角的关系。
　　圆是一种几何图形。
　　根据定义，通常用圆规来画圆。
　　同圆内圆的直径、半径。