tan和角公式

tan和角公式

　　tan和角公式tan（α-β）=（tanα-tanβ）/（1+tanαtanβ）。
　　和角公式又称三角函数的加法定理是几个角的和（差）的三角函数通过其中各个角的三角函数来表示的关系。
　　三角函数是数学中属于初等函数中的超越函数的一类函数。

tan的两角和公式

　　tan的两角和公式：tan(α+β)=(tanα+tanβ)/(1-tanαtanβ)。
　　tan指正切，在Rt△ABC（直角三角形）中，∠C=90°，AB是∠C的对边c，BC是∠A的对边a，AC是∠B的对边b，正切函数就是tanB=b/a，即tanB=AC/BC。
　　

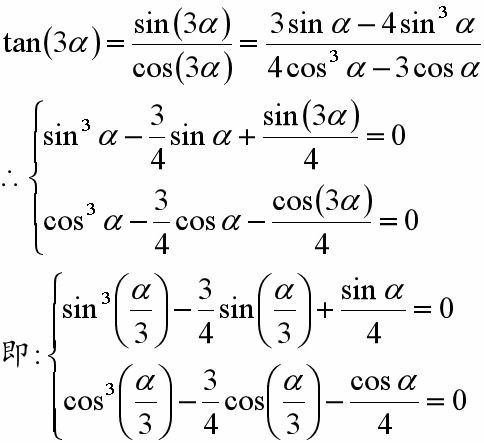
正切和角公式是多少?

　　正切和角公式是：tan(A+B) = (tanA+tanB)/(1-tanA*tanB)，当A=B时，就是倍角公式：tan2A=2tanA/(1-^2)。
　　两角和（差）公式包括两角和差的正弦公式、两角和差的余弦公式、两角和差的正切公式。
　　两角和与差的公式。

tan和角公式

　　tan(2kπ+α)=tanα cot(2kπ+α)=cotα 公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)=-sinα cos(π+α)=-cosα tan(π+α)=tanα cot(π+α)=cotα 。

tan的和角公式怎么推导出来的

　　tan(A+B)=sin(A+B)/cos(A+B)=(sinαcosβ+cosαsinβ)/(cosαcosβ-sinαsinβ)同时除以cosAcosB =(tanA+tanB)/(1-tanAtanB)