正弦定理公式
正弦定理公式是:a/sina=b/sinb=c/sinc=2R。
正弦值是在直角三角形中,对边的长比上斜边的长的值。
任意锐角的正弦值等于它的余角的余弦值,任意锐角的余弦值等于它的余角的正弦值。
通常用符号sin表示。
正弦sinθ也可以。
正弦定理和余弦定理是什么?
正弦定理是三角学中的一个基本定理,它指出“在任意一个平面三角形中,各边和它所对角的正弦值的比相等且等于外接圆的直径”,即a/sinA=b/sinB=c/sinC= 2r=D(r为外接圆半径,D为直径)。
余弦定理是三角形边角关系的。
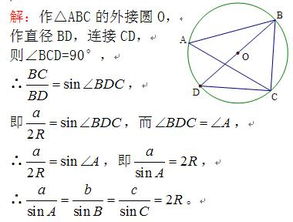
正弦定理是什么呢?
正弦定理 在任意一个平面三角形中,每条边跟它所对角的正弦值的比相等且等于外接圆的直径”。
即 a/sinA = b/sinB = c/sinC = 2r = D 其中,r为外接圆的半径,D 为外接圆的直径。
什么是正弦定理?
正弦定理是三角学中的一个定理。
它指出了三角形三边、三个内角以及外接圆半径之间的关系。
正弦定理是什么?
正弦定理(Sine theorem);正弦定理的应用:(1)已知三角形的两角与一边,解三角形 (2)已知三角形的两边和其中一边的对角,解三角形 公式的变形:a=2RsinA,b=2RsinB,c=2RsinC,a:b:c=sinA:sinB:sinC 直角三角。
