反函数定义是什么?
反函数定义:设函数y=f(x)的定义域是D,值域是f(D)。
如果对于值域f(D)中的每一个y,在D中有且只有一个x使得g(y)=x,则按此对应法则得到了一个定义在f(D)上的函数,并把该函数称为函数y=f(x)的反函数。
反。
反函数的定义及性质
如题 另外帮忙列出几个例题 详细讲解的反函数定义:一般地,对于函数y=f(x),设它的定义域为D,值域为A,如果对A中任意一个值y,在D中总有唯一确定的x值与它对应,且满足y=f(x),这样得到的x关于y的函数叫做y=f(x)的反函数,记作x=f-1(y),通。
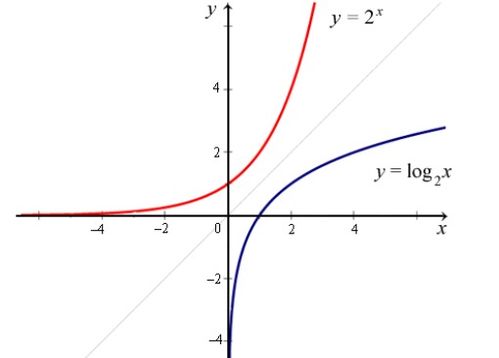
反函数的意思反函数的意思是什么
反函数的词语解释是:设函数y=f(x)的定义域为a,值域为c,从y=f(x)中解出x,得x=φ(y)。
如果对于c中每一个y的值,通过x=φ(y),在a中都有唯一确定的x值与它对应,那么x=φ(y)就表示x是自变量y的函。
反函数的定义是什么
所谓反函数就是将原函数中自变量与变量调换位置,用原函数的变量表示自变量而形成的函数。
存在反函数的条件是原函数必须是一一对应的(不一定是整个数域内的)。
函数的定义 一般地,如果x与y关于某种对应关系f(x)相对应,y=f(x)。
则。
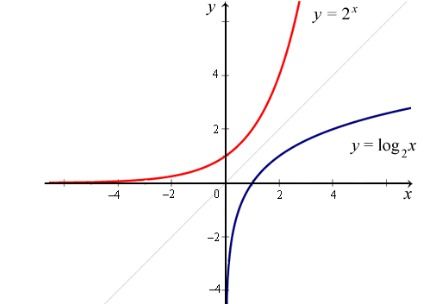
反函数的定义是什么?
,则函数f(x)是偶函数且有反函数,其反函数的定义域是{C},值域为{0})。
奇函数不一定存在反函数,被与y轴垂直的直线截时能过2个及以上点即没有反函数。
若一个奇函数存在反函数,则它的反函数也是奇函数。
