有界数列一定收敛吗?
有界的数列不一定收敛。
例如:已知数列{(-1)^n}是有界的,但它却是发散的,换句话说有界是数列收敛的必要条件而不是充分条件。
在一些一般性叙述中,收敛和收敛性这两个词(在外语中通常是同一个词)有时泛指函数或数列是。
有界数列是否一定收敛
有界数列不一定收敛,比如数列{b(n)},b(n)=(-1)^n,|b(n)|<=1 {b(n)}有界,b(n)为摆动数列,但是不收敛。
数列中的每一项均不超过一个固定的区间,其中分上界和下界。
假设存在定值a,任意n有{An(n为下角。
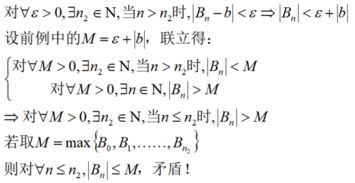
有界的数列一定是收敛数列吗
有界的数列不一定收敛,最简单的例子xn=sin(n),或者xn=(-1)^n,它们都是有界数列,但n→∞时,xn的极限不存在,所以不收敛。
收敛数列与其子数列间的关系:1、子数列也是收敛数列且极限为a恒有|Xn|<M。
2、若已知一。
有界数列就收敛吗?
无界数列一定发散,所以有界是收敛的必要条件,但是有界数列不一定收敛。
显然是有界的,但也是发散的。
所以有界不是收敛的充分条件。
有界数列是指任一项的绝对值都小于等于某一整数的数列。
有界数列是指数列中的每一项均不超过。

有界数列一定收敛吗?
有界数列不一定收敛。
有界数列,是数学领域的定理,是指任一项的绝对值都小于等于某一正数的数列。
有界数列是指数列中的每一项均不超过一个固定的区间,其中分上界和下界。
定义 若数列{Xn}满足:对一切n有Xn≤M(其中M是。
