抛物线的切线方程是什么?
若x²=2py,则切线x0x=p(y0+y)。
3、已知切线斜率k 若y²=2px,则切线y=kx+p/(2k)。
若x²=2py,则切线x=y/k+pk/2(y=kx-pk²/2)。
抛物线性质若椭圆的方程为 ,。
抛物线的切线方程是什么?
抛物线切线方程:1、已知切点Q(x0,y0),若y²=2px,则切线y0y=p(x0+x);若x²=2py,则切线x0x=p(y0+y)等。
2、已知切点Q(x0,y0)若y²=2px,则切线y0y=p(x0+x)。
若。
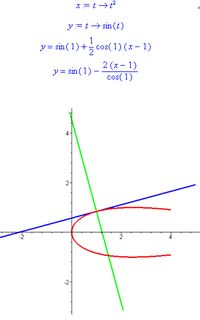
抛物线的切线方程怎么求
抛物线的切线方程是y'=2ax+b,切线方程是研究切线以及切线的斜率方程,涉及几何、代数、物理向量、量子力学等内容。
是关于几何图形的切线坐标向量关系的研究,分析方法有向量法和解析法。
平面内,到定点与定直线的距离相等的点。
抛物线的切线方程是什么?
抛物线的切线方程没有公式 标准抛物线分为 y^2=2px x^2=2py y^2=-2px x^2=-2py,p>0 等四种类型,3,4项是1,2项的延伸 对于抛物线方程为y^2=2px,抛物线上一点M(a,b)的切线 可设切线方程为y-b=k(x-a。
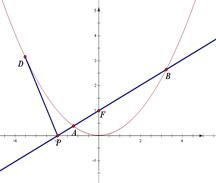
抛物线切线方程公式
已知切点Q(x0,y0),若y=2px,则切线y0y=p(x0+x);若x=2py,则切线x0x=p(y0+y)。
在平面内,到定点与定直线的距离相等的点的轨迹叫做抛物线。
抛物线是指平面内到一个定点F(焦点)和一条定直线l(准线)距离。
