基本函数积分公式。
基本函数积分公式如下图所示:积分是微分的逆运算,即知道了函数的导函数,反求原函数。
在应用上,积分作用不仅如此,它被大量应用于求和,通俗的说是求曲边三角形的面积,这巧妙的求解方法是积分特殊的性质决定的。
主要分为。
24个基本积分公式
24个基本积分公式:1、∫kdx=kx+C(k是常数)。
2、∫x^udx=(x^u+1)/(u+1)+c。
3、∫1/xdx=ln|x|+c。
4、∫dx=arctanx+C21+x1。
5、∫dx=arcsinx+C21x。
(配图1)24个基本积分公式还有如下:6、∫cosxdx。
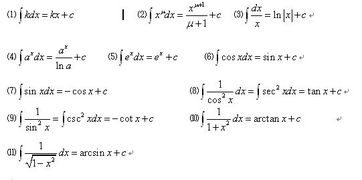
积分基本公式
常用的积分公式有 f(x)->∫f(x)dx k->kx x^n->[1/(n+1)]x^(n+1)a^x->a^x/lna sinx->-cosx cosx->sinx tanx->-lncosx cotx->lnsinx
积分的基本公式有哪些?
常用的积分公式有:∫kdx=kx+C,∫xudx=u+1xu+1+C,∫x1dx=ln∣x∣+C,∫exdx=ex+C,∫axdx=lnaax+C,∫cosxdx=sinx+C,∫sinxdx=−cosx+C,∫1+x21dx=arctanx+C=−arccotx+C,∫1&#。
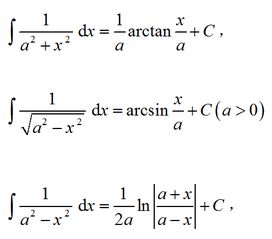
积分的公式有哪些?
基本积分公式如下:1、牛顿-莱布尼茨公式,又称为微积分基本公式。
2、格林公式,把封闭的曲线积分化为区域内的二重积分,它是平面向量场散度的二重积分。
3、高斯公式,把曲面积分化为区域内的三重积分,它是平面向量场散度的三。
