行列式按行列展开法则
行列式可按行或列展开,于是每个行列式可以表成它的某一行(或某一列)的每个元素与它对应元素的代数余子式乘积的和,即 D= ai1Ai1+ ai2Ai2+ ai3Ai3 (i= 1, 2,3) , (1)D= a1jA1j+ a2jA2j+ a3jA3j (。
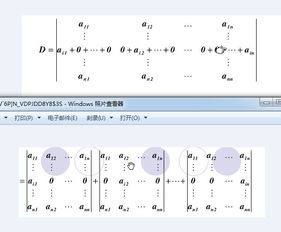
行列式按行(列)展开原则
如果全面的话请多讲一些不需要符合什么条件,只要 行列式存在,就能按这个方式展开。
(当然,为了化简行列式,通常尽量按0和1比较多的那一行(或列)来展开。
)展开方法:用该行(或列)各元素乘以该元素对应的《代数余子式》,然后求和。
(这样,。
行列式展开的公式是什么?
行列式按行展开的定理是拉普拉斯定理的一种简单情况,该行各元素分别乘以相应代数余子式求和,就等于行列式的值.例如:D=a11·A11+a12·A12+a13·A13+a14·A14 Aij是aij对应的代数余子式 Aij=(-1)^(i+j)·MijMij是ai。

行列式按行(列)展开
那一列(行)的数值符合什么条件时能展开不需要符合什么条件,只要 行列式存在,就能按这个方式展开。
(当然,为了化简行列式,通常尽量按0和1比较多的那一行(或列)来展开。
)展开方法:用该行(或列)各元素乘以该元素对应的《代数余子式》,然后求和。
(这样,。
