柯西不等式公式有哪些
1、二维形式:(a^2+b^2)(c^2 + d^2)≥(ac+bd)^2 等号成立条件:ad=bc 2、三角形式:√(a^2+b^2)+√(c^2+d^2)≥√[(a-c)^2+(b-d)^2]等号成立条件:ad=bc 3、向量形式:|α||β|≥|。
什么是柯西不等式?
柯西不等式公式:√(a^2+b^2)≥(c^2+d^2)。
柯西不等式是由柯西在研究过程中发现的一个不等式,其在解决不等式证明的有关问题中有着十分广泛的应用,所以在高等数学提升中与研究中非常重要,是高等数学研究内容之。
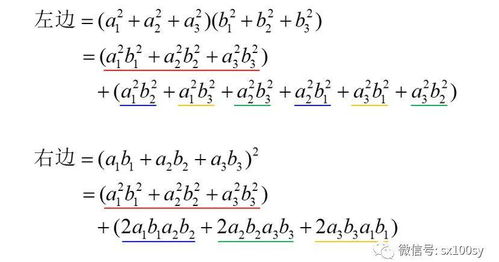
柯西不等式的公式是什么?
等号成立条件:a1:b1=a2:b2=…=an:bn,或ai、bi均为零。
1.柯西不等式的特点:左边是平方和的积,简记为方和积,右边是乘积和的平方。
2.柯西不等式的直接应用。
例:已知x,y满足x+3y=4,求4x2+y2的最小值。
分析。
柯西不等式是什么?
柯西不等式6个基本题型如下:1、二维形式:(a^2+b^2)(c^2 + d^2)≥(ac+bd)^2 等号成立条件:ad=bc 2、三角形式:√(a^2+b^2)+√(c^2+d^2)≥√[(a-c)^2+(b-d)^2]等号成立条件:ad=bc 。

柯西不等式一般形式是什么?
柯西不等式的一般形式如下陈述:在数学中,柯西不等式(Cauchy-Schwarz inequality)在线性代数、数学分析、概率论等领域中都是非常有用的不等式,它被认为是数学中最重要的不等式之一。
基本简介 柯西(CauchyAugustin-Louis,。
