指数函数与对数函数的转换公式
对数函数的一般形式为 y=logax,它实际上就是指数函数的反函数(图象关于直线y=x对称的两函数互为反函数),可表示为x=a^y。
因此指数函数里对于a存在规定——a>0且a≠1,对于不同大小a会形成不同的函数图形:关于X。
指数和对数怎么互换
对数和指数的转换公式是:a^y=xy=log(a)(x)。
对数函数的一般形式为 y=logax,它实际上就是指数函数的反函数,图象关于直线y=x对称的两函数互为反函数,可表示为x=a^y。
因此指数函数里对于a存在规定:a>0且a≠1。
指数和对数怎么互换
指数和对数的转换公式表示为x=a^y。
对数与指数之间的关系:当a大于0,a不等于1时,a的X次方=N等价于log(a)N=x。
log(a^k)(M^n)=(n/k)log(a)(M)(n属于R)。
换底公式(很重要):log(a)(N)=log(b)(。
对数和指数的运算公式分别是什么?
指数的运算公式:1、[a^m]×[a^n]=a^(m+n) 【同底数幂相乘,底数不变,指数相加】2、[a^m]÷[a^n]=a^(m-n) 【同底数幂相除,底数不变,指数相减】3、[a^m]^n=a^(mn) 【幂的乘方,底数不变,指数。
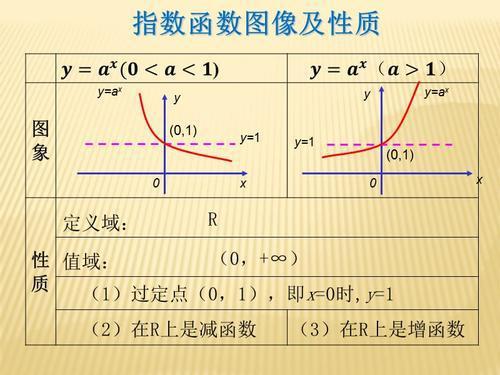
对数和指数的转换公式是什么?
公式如下:对数函数的一般形式为 y=logax,它实际上就是指数函数的反函数(图象关于直线y=x对称的两函数互为反函数),可表示为x=a^y,因此指数函数里对于a存在规定——a>0且a≠1,对于不同大小a会形成不同的函数。
