欧拉公式的推导过程
R+ V- E= 2就是欧拉公式。
欧拉公式怎么推导?
欧拉公式不是推导出来的,欧拉公式就是一个定义式!如下:在复变函数中,设z是一个作为宗量(也就是自变量)的复数,则z=x+iy。
则定义w=f(z)=e^z=e^(x+iy)=(e^x)(e^iy)=(e^x)(cosy+isiny)。
请注意上。
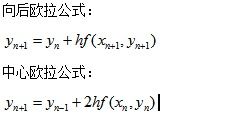
欧拉公式推导 欧拉公式推导简述
欧拉公式推导如下:1. 欧拉公式是e^ix=cosx+isinx, e是自然对数的底,I是虚数单位。
将三角函数的定义域扩展到复数,建立了三角函数与指数函数的关系。
它在复变函数理论中起着非常重要的作用。
2. e^ix=cosx+isinx的证明。
欧拉公式的推导过程
将公式里的x换成-x,得到:e^-ix=cosx-isinx,然后采用两式相加减的方法得到:sinx=(e^ix-e^-ix)/(2i),cosx=(e^ix+e^-ix)/2.tanx=[e^(ix)-e^(-ix)]/[ie^(ix)+ie^(-ix)]此时三角函数定义域已。
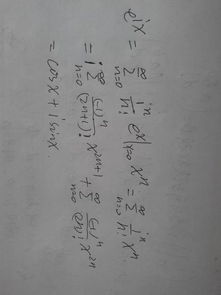
欧拉公式推导
尝欧拉公式:对于任意多面体(即各面都是平面多边形并且没有洞的立体),假 设F,E和V分别表示面,棱(或边),角(或顶)的个数,那么 F-E+V=2。
试一下用拓朴学方法证明关于多面体的面、棱、顶点数的欧拉公式。
证。
