arccotx的导数是什么?
arctanx的导数是1/1+x²,设y=arctanx,则x=tany,因为arctanx′=1/tany′,且tany′=(siny/cosy)′=cosycosy-siny(-siny)/cos²y=1/cos²y,则arctanx′=cos²y=cos²y/sin&#。

arccotx的导数是多少
f(x)=arccotx,则导数f′(x)=-1/(1+x²).证明如下:设arccotx=y,则 coty=x 两边求导,得 (-csc²y)·y′=1,即y′=-1/csc²y=-1/(1+cot²y),因此,y′=f′(x)=-1/(1+。
arcsecx 导数
arcsecx的导数:1/[x√(x²-1)]。
解答过程如下:设y=arcsecx,则secy=x。
两边求导得:secytanyy '=1 得y'=1/[secytany]=1/[secy√(sec²y-1)=1/[x√(x²-1)]。
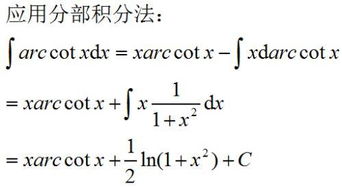
【高数求导】求arccotx的求导过程!
(tany)'=sec^2y 有反函数求导公式dy/dx=1/(dx/dy)得 (arctanx)'=1/(tany)'=1/sec^2y 又sec^2y=1+tan^2y=1+x^2 所以(arctanx)'=1/(1+x^2)又arccotx=pi/2-arctanx 将(arctanx)'=1/(1+x^2。
