求不定积分 1/xlnx
由此可知,如果F(x)是f(x)在区间I上的一个原函数,那么F(x)+C就是f(x)的不定积分,即∫f(x)dx=F(x)+C。
因而不定积分∫f(x) dx可以表示f(x)的任意一个原函数。
xlnx分之一的不定积分
xlnx分之一的不定积分的解答过程为∫1/(xlnx) dx=∫dlnx/lnx=ln(lnx)+C。
在微积分中,一个函数f 的不定积分、原函数或反导数,是一个导数等于f 的函数 F,即F′= f。
不定积分和定积分间的关系由微积分基本。
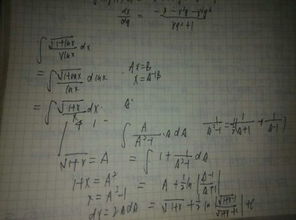
1/xlnx的不定积分怎么求,具体步骤?
如果是∫1/x *lnxdx 即得到 ∫ lnx d(lnx)=1/2 ln²x +C 而如果是∫1/(x *lnx)dx 则得到 ∫ 1/lnx d(lnx)=ln|lnx| +C,C为常数
1/xlnx的不定积分
∫1/(xlnx) dx =∫dlnx/lnx =ln(lnx)+C 很高兴为您解答,祝你学习进步!【the1900】团队为您答题。
有不明白的可以追问!如果您认可我的回答。
请点击下面的【选为满意回答】按钮,谢谢!

计算不定积分∫ (1/xlnx)dx
∫ (1/xlnx)dx =∫lnxdlnx =(lnx)²/2+C
