微分方程的通解公式

　　常微分方程通解公式是：y=y(x)。
　　隐式通解一般为f(x,y)=0的形式，定解条件，就是边界条件，或者初始条件。
　　常微分方程，属数学概念。
　　学过中学数学的人对于方程是比较熟悉的。
　　在初等数学中就有各种各样的方程，,比如。

　　微分方程的通解公式：1、一阶常微分方程通解 dydx+p(x)y=0dydx+p(x)y=0。
　　2、齐次微分方程通解 y=ce−∫p(x)dx。
　　3、非齐次微分方程通解 y=e−∫p(x)dx(c+∫q(x)e∫p(x)dxdx)。
　　4、二阶常。

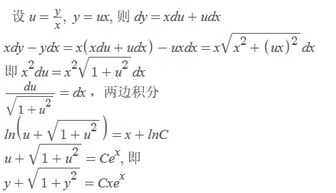
微分方程的通解公式

微分方程通解公式

　　微分方程通解公式是dy/dx=1/(x+y)，微分方程是指含有未知函数及其导数的关系式。
　　解微分方程就是找出未知函数。
　　微分方程是伴随着微积分学一起发展起来的。
　　微积分学的奠基人Newton和Leibniz的著作中都处理过与微分方程有关的。

　　第一种：y=C1cos2x+C2sin2x-xsin2x。
　　由y2-y1=cos2x-sin2x是对应齐方程的解可推出cos2x、sin2x均为齐方程的解。
　　第二种：通解是一个解集，包含了所有符合这个方程的解；n阶微分方程就带有n个常数，与是否线性无关。

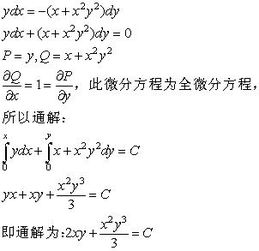
二阶微分方程的3种通解公式是什么?

　　解：设y'-y/x=0，有dy/y=dx/x，两边积分有y=x。
　　再设方程的通解为y=xu(x)，则y'=u(x)+u'(x)x，代入原方程，经整理有，u'(x)=(-2lnx)/x^2。
　　两边再积分有，u(x)=(2/x)(lnx+1)+C。
　　∴原方程的。