逆矩阵怎么求?
逆矩阵的求法:1、利用定义求逆矩阵 设A、B都是n阶方阵, 如果存在n阶方阵B 使得AB=BA=E, 则称A为可逆矩阵, 而称B为A的逆矩阵。
2、运用初等行变换法 将一n阶可逆矩阵A和n阶单位矩。
怎么求逆矩阵?
逆矩阵求法有三种,分别是伴随矩阵法、初等变换法和待定系数法。
一、伴随矩阵法。
根据逆矩阵的定义(对于n阶方阵A,如果有一个n阶方阵B满足AB=BA=E,则A是可逆的。
),可以得出逆矩阵的计算公式:A^(-1)=1/|A|乘以。

怎么求逆矩阵?
一般用初等行变换,来求,对增广矩阵A|E,同时施行初等行变换,化成E|A^-1;在原矩阵的右侧接写一个四阶单位矩阵,然后对扩展矩阵施行初等行变换,使前面的四阶矩阵化为单位矩阵,则右侧的单位矩阵就化为了原来前面的逆。
逆矩阵怎么求?
计算公式:A^(-1)=(︱A︱)^(-1) A﹡(方阵A的行列式的倒数乘以A的伴随矩阵)。
这个公式在矩阵A的阶数很低的时候(比如不超过4阶)效率还是比较高的,但是对于阶数非常高的矩阵,通常我们通过对2n*n阶矩阵[A In]。
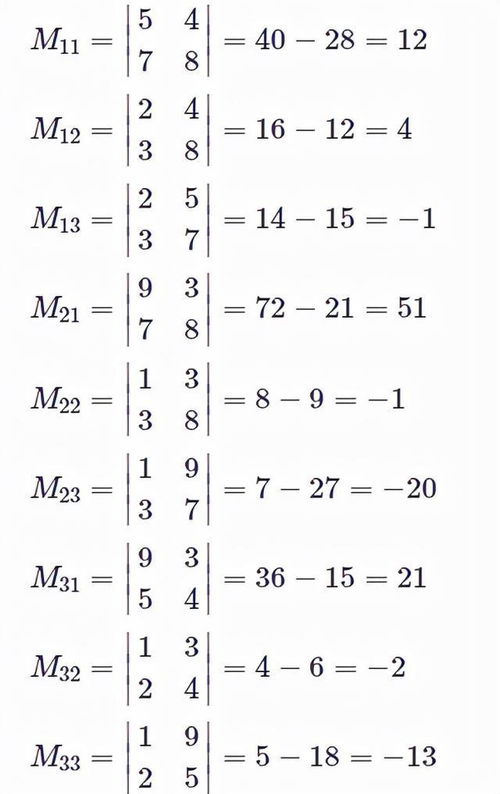
求逆矩阵的方法
典型的矩阵求逆方法有:利用定义求逆矩阵、初等变换法、伴随阵法、恒等变形法等。
一般有2种方法。
1、伴随矩阵法。
A的逆矩阵=A的伴随矩阵/A的行列式。
2、初等变换法。
A和单位矩阵同时进行初等行(或列)变换,当A变成单位。
