lnx的原函数是什么?
求lnx的原函数就是求lnx的不定积分。
直接积分法:令t=lnx,则x=e^t,dx=e^tdt.∫lnxdx=∫t*e^tdt=∫td(e^t)=t*e^t-∫e^tdt=t*e^t-e^t+C=(t-1)e^t+C=(lnx-1)x+C。
不定积分的公式 1、∫ a 。
lnX的原函数是什么?
即lnx的原函数是:xlnx-x+c。
2、使用分部积分法:已知[f(x)g(x)]'=f'(x)g(x)+f(x)g'(x)积分得f(x)g(x)=∫f'(x)g(x)+∫f(x)g'(x)故∫f'(x)g(x)=f(x)g(x)-∫f(x)g'(x)∫lnx dx。
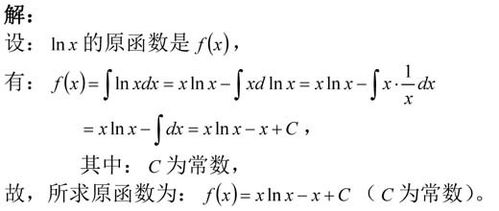
lnx的原函数是什么
即lnx的原函数是:xlnx-x+c.
如何求lnx的原函数
∫lnxdx=(lnx-1)x+C。
C为积分常数。
解答过程如下:求lnx的原函数就是对lnx进行不定积分。
∫lnxdx =xlnx-∫xdlnx =xlnx-x+C =(lnx-1)x+C
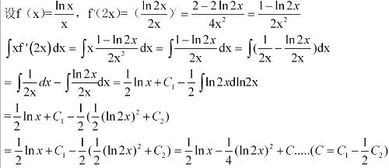
lnx的原函数
“lnx原函数是∫lnxdx=xlnx-∫dx=xlnx-x+C;用分部积分法:(lnxdx)的原函数=xlnx-(x(lnx)')的原函数=xlnx-(1)的原函数=xlnx-x+C;∫1nxdx=xlnx-x+c其中c为常数,以下为推导公式。
”∫1nxdx=xlnx-x+。
