月牙定理的详细过程
定理:新月形AECF可用等价平方表示。
证明;由于∠ACB内接于半圆,所以,∠ACB是直角。
根据“边角边”勾股定理,就得到因为AB是半圆ACB的直径,AC是半圆AEC的直径,所以,我们可以应用上述第三条原理,即得到也就是说,半圆AEC。
月牙定理
怎么验证c边上的半圆面积为π(c/2)^2/2③ 由①式可知②③式相等 ②③同减去两个弓形面积即得月牙定理.
月牙定理的基本简介
首先,AB,且与半圆相交于C,并连接AC与BC。
平分AC于D,然后,以D为圆心,以AD为半径作半圆AEC,这样,就形成了新月形AECF希波克拉底的证明方法既简单又高明。
首先,他必须证实所论证的新月形与图中阴影部分的△AOC面积。
希波克拉蒂月牙问题的理解
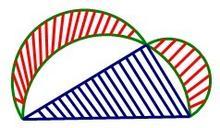
以直角三角形两直角边为直径向外作两个半圆,以斜边为直径向内作半圆,则三个半圆所围成的两个月牙(希波克拉底月牙)面积的和等于该直角三角形的面积。
这个定理叫作希波克拉底的“月牙定理”(Hippocrate's Theorem)。
月牙定理及其图形
以直角三角形两条直角边向外做两个半圆,以斜边向内做半圆,则三个半圆所围成的两个月牙型面积之和等于该直角三角形的面积。
