虚数i的运算公式
虚数i的运算公式:(a+bi)±(c+di)=(a±c)+(b±d)i。
在数学中,虚数就是形如a+b*i的数,其中a,b是实数,且b≠0,i²=-1。
虚数这个名词是17世纪著名数学家笛卡尔创立,因为当时的观念认为这是真。
虚数的公式,运算规则? 尽可能多吧.
cos(i) = cosh(1) = (e + 1/e)/2 = (e^2 + 1) /2e = 1.54308064.i的正弦是虚数:sin(i) = sinh(1) * i = (e - 1/e)/ 2} * i = 1.17520119 i.i,e,π,0和1的奇妙关系:e^(i*π)+。
虚数的实际意义及运算公式
在数学中,虚数就是形如a+b*i的数,其中a,b是实数,且b≠0,i²=-1。
接下来给大家分享虚数的实际意义和运算公式。
虚数的实际意义 一切事物的值都可表示为:a+bi,而不是单有实数。
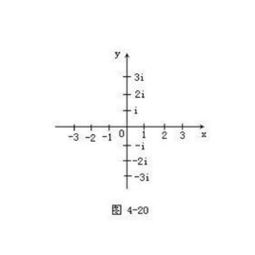
我们可以在平面直角坐标系。
虚数i的运算公式大全
虚数i的四则运算公式 (a+bi)±(c+di)=(a±c)+(b±d)i (a+bi)(c+di)=(ac-bd)+(ad+bc)i (a+bi)/(c+di)=(ac+bd)/(c²+d²)+(bc-ad)i/(c²+d²)r1(isina+cosa)。
高中数学虚数i的运算
虚数i的三角函数公式:1、sin(a+bi)=sin(a)cos(bi)+sin(bi)cos(a)=sin(a)cosh(b)+isinh(b)cos(a)2、cos(a-bi)=cos(a)cos(bi)+sin(bi)sin(a)=cos(a)cosh(b)+isinh(b)sin(a)3、tan(a+bi)=。
