空间中过z轴的平面方程怎么表示
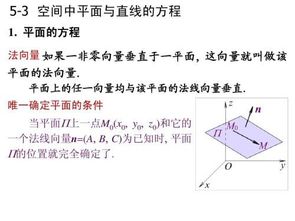
“平面方程”是指空间中所有处于同一平面的点所对应的方程,其一般式形如Ax+By+Cz+D=0。
当平面过 z 轴时,所有的z都等于0,所以不含z,因此C = 0 ,同时,由于平面过Z轴,因此该平面必定经过原点,即x=y=z=0。
通过z轴和点(-3,1,-2) 求平面方程
第一种方法:过z轴的平面方程系是:ax+by = 0又平面过点(-3,1,-2)∴-3a+b=0b=3a ∴x+3y=0∴ 通过z轴和点(-3,1,-2)的平面方程是x+3y=0 第二种方法:设方程为 Ax+BY=0 【通过z轴的平面的通式】代。
通过z轴的平面怎么画
画z轴的方法如下首先过z轴的平面方程系是:ax+by=0又平面过点(-3,1,-2)即x=-3、y=1;在带入:-3a+b=0b=3a所以:ax+3ay=0a(x+3y)=0所以通过z轴和点(-3,1,-2)的平面方程是x+3y=0 。
平面通过z轴,方程为什么设成:Ax+By=0
设平面方程为Ax+By+Cz=D,z轴的方向向量为(0,0,1),平面过z轴则有,平面的方向向量与z轴的方向向量平行且平面过原点:(A,B,C).(0,0,1)=0得C=0,且过原点(0,0,0),代入平面方程,可得D=0。
因此平面方程。
高等数学中一个知识。一个过z轴的平面需要满足什么条件?是c等于0吗
过z轴的平面方程一定是C=0和D=0,为Ax+By=0。
只有C=0的平面方程是平行于z轴的。
